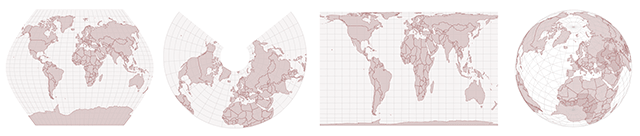
Today I want to introduce as3-proj, an actionscript port of the java map projection library by Jerry Huxtable, which is itself an partial port of the PROJ.4 library. It’s basically a huge set of over sixty map projection classes which you can use to convert geographical coodinates (pairs of latitude and longitude values) into screen coordinates.

Usage example

You can use the projection classes like this:

var lat:Number, lng:Number, proj:Projection, p:Point;
lat = 40.2302; // degrees
lng = 24.32434; // degrees
proj = new RobinsonProjection();
proj->initialize();
p = proj->project(lat, lng, new Point());
// p contains converted values in metres

Demonstration

I built a sample application that shows static world maps in different map projection. You can switch the map projection using the menu at the bottom. Also you can filter out some map projections, e.g. to only display rectilinear map projections. The visualization of some projections (like the Orthographic Projection) still need a little more coding to be perfect (eg. removal of hidden lines and faces), but this was out of the scope of this demo.

Supported projections

You find a alphabetically sorted list of all included map projections and their properties below.

projection has invers parallels are parallels is rectilinear is conformal is equal area

PROJECTION	HAS INVERS	PARALLELS ARE PARALLELS	IS RECTILINEAR	IS CONFORMAL	IS EQUAL AREA
Airy’s Minimum-Error Azimuthal	no	no	no	no	no
Aitoff	no	no	no	no	no
Albers Equal Area	yes	no	no	yes	yes
Boggs Eumorphic	no	yes	no	no	yes
Bonne	yes	no	no	no	yes
Cassini	yes	no	no	no	no
Central Cylindrical	yes	yes	yes	yes	no
Collignon	yes	yes	no	no	yes
Craster Parabolic (Putnins P4)	yes	no	no	no	yes
Cylindrical Equal Area	yes	yes	yes	yes	no
Denoyer Semi-elliptical	no	yes	no	no	no
Eckert I	yes	yes	no	no	no
Eckert II	yes	yes	no	no	no
Eckert IV	yes	yes	no	no	no
Eckert V	yes	yes	no	no	no
Euler	yes	no	no	yes	no
Fahey	yes	yes	no	no	no
Foucaut Sinusoidal	yes	yes	yes	yes	no
Gall Stereographic	yes	yes	yes	yes	no
Gall-Peters	yes	yes	yes	yes	yes

projection has invers parallels are parallels is rectilinear is conformal is equal area

PROJECTION	HAS INVERS	PARALLELS ARE PARALLELS	IS RECTILINEAR	IS CONFORMAL	IS EQUAL AREA
Ginsburg VIII (TsNIIGAiK)	no	yes	no	no	no
Goode Homolosine	yes	yes	no	no	yes
Hammer & Eckert-Greifendorff	no	no	no	no	yes
Hatano Asymmetrical Equal Area	yes	yes	no	no	no
Kavraisky V	yes	yes	no	no	yes
Lagrange	no	no	no	yes	no
Lambert Conformal Conic	yes	no	no	yes	no
Lambert Equal Area Conic	yes	no	no	yes	yes
Landsat	no	no	no	no	no
Larrivée	no	no	no	no	no
Laskowski Tri-Optimal	no	no	no	no	no
Loximuthal	yes	yes	no	no	no
McBride-Thomas Flat-Polar Parabolic	yes	yes	no	no	no
McBryde-Thomas Flat-Polar Quartic	yes	yes	no	no	no
McBryde-Thomas Flat-Polar Sine I	yes	yes	no	no	no
McBryde-Thomas Flat-Polar Sine II	yes	yes	no	no	no
Mercator	yes	yes	yes	yes	no
Miller Cylindrical	yes	yes	yes	yes	no
Mollweide	yes	yes	no	no	yes
Murdoch I	yes	no	no	yes	no

projection has invers parallels are parallels is rectilinear is conformal is equal area

PROJECTION	HAS INVERS	PARALLELS ARE PARALLELS	IS RECTILINEAR	IS CONFORMAL	IS EQUAL AREA
Murdoch II	yes	no	no	yes	no
Murdoch III	yes	no	no	yes	no
Nell	yes	yes	no	no	yes
Nell-Hammer	yes	yes	no	no	no
Nicolosi Globular	no	no	no	no	no
Orthographic Azimuthal	yes	no	no	no	no
Perspective Conic	yes	no	no	yes	no
Plate Carrée	yes	yes	yes	yes	no
Putnins P’4	yes	yes	no	no	yes
Putnins P’5	yes	no	no	no	no
Craster Parabolic (Putnins P4)	yes	no	no	no	yes
Putnins P5	yes	no	no	no	no
Quartic Authalic	yes	yes	no	no	yes
Robinson	yes	yes	no	no	no
Sinusoidal	yes	yes	no	no	no
Transverse Central Cylindrical	no	no	no	no	no
Transverse Cylindrical Equal Area	yes	no	no	no	yes
Tissot	yes	no	no	yes	no
Urmaev Flat-Polar Sinusoidal	yes	no	no	no	no
van der Grinten (I)	yes	no	no	no	no

projection has invers parallels are parallels is rectilinear is conformal is equal area

PROJECTION	HAS INVERS	PARALLELS ARE PARALLELS	IS RECTILINEAR	IS CONFORMAL	IS EQUAL AREA
Vitkovsky	yes	no	no	yes	no
Wagner II	yes	no	no	no	no
Wagner III	yes	yes	no	no	no
Wagner IV	yes	yes	no	no	no
Wagner V	yes	yes	no	no	no
Wagner VII	no	no	no	no	yes
Werenskiold I	yes	yes	no	no	yes
Winkel Tripel	no	no	no	no	no

The following projection are also included but are a bit buggy yet. Maybe someone with more knowledge about map projection math is able to stop those formulas from throwing weird exceptions.

projection has invers parallels are parallels is rectilinear is conformal is equal area

PROJECTION	HAS INVERS	PARALLELS ARE PARALLELS	IS RECTILINEAR	IS CONFORMAL	IS EQUAL AREA
August Epicycloidal	no	no	no	yes	no
Bipolar Conic	yes	no	no	no	no
Equidistant Azimuthal	yes	no	no	no	no
Lambert Equal Area Azimuthal	yes	no	no	no	yes
Space-oblique Mercator	yes	no	no	no	no

Since I only tested the one-way projection of geographic coordinates into screen coordinates there still might be some bugs on the inverse projections. The java code of the map projection library had a few errors. Hope the classes are helpful anyway.

Download & License

The source code of as3-proj is released under the Apache License.

You can download the sources from my bitbucket account. Here is a direct link to the zipped sources.

Comments

vtstarin (Apr 24, 2010)

Hi Thanks for porting PROJ.4 to as3.

For eg (-180,90)= (log,lat) in RobinsonProjection (x=-125066398.48278639, y=-751566.9221849588)

How can you I convert this X Y mapping coordinate to X Y pixel coordinate for Image (3600x1800 pixels)?

Thank you again for your time and effort.

vtstarin (Apr 25, 2010)

Thank you Gregor.

I still can’t work around how is it done?. A short tutorial would be really my life savior.

Gregor Aisch (Apr 24, 2010)

I use the DataView class. The constructor takes two rectangles. The first is the bounding box of all projected points (you have to iterate over all projected coordinates and store the minimum and maximum values of x and y). The second rectangle is your target screen area. By the way, I’ll publish a short tutorial showing this procedure in the next few days..

regards, Gregor

Tutorial: Rendering a World Map in ActionScript | vis4.net (Sep 16, 2010)

[…] we must chose and initialize a map projection. I’m using the Wagner V projection of the as3-proj library. var projection:Projection = new Wagner5Projection(); […]

Gregor (Jul 23, 2010)

Hi Chris,

Yoh have to multiply every projected y-coordinate by -1 before drawing. Assumedly the projection fomulas weren’t designed for screen output but for print output and thus refer to a mirrored coordinate system.

The tutorial I mentioned is already there, you can find it here.

Chris (Jul 25, 2010)

Gregor, Thanks for the quick response and link to the tutorial. I ended up writing my own Robinson projection function in AS3 which it looks like was a duplication of work but definitely helped make me more familiar with what was going on. Chris

Chris (Jul 22, 2010)

Thanks for your work on this! I’m working with the Robinson projection and I’m confused why the sign of the X/Y coordinates differ from the sign of latitude and longitude. For example:

(-180,90)= (log,lat) in RobinsonProjection (x=-125066398.48278639, y=-751566.9221849588)

Aren’t the X/Y coordinates also starting from an origin at the central meridian and the equator? Shouldn’t the sign for y and latitude be the same?

Also…if you get the chance to post that tutorial it’d be a life saver here too.

Chris (Sep 29, 2010)

I was getting incorrect values from your Robinson Projection so I wrote my own and open sourced the code at: http://www.flashmap.org/robinson-projection-in-as3-gpl/

Rendering SVG Country Maps in Python — vis4.net (Oct 26, 2011)

[…] Therefore, I would have to port parts of the PROJ.4 code to JavaScript, which is something I’ve done before in ActionScript and actually don’t want to do again. Instead, I found a nice and simple Python implementation of […]

Chen (Nov 22, 2011)

I use Proj4 libray in my C++ project, when i try to use this AS3 version i found some projection types were removed, like Transverse Mercator, any ideas about this?

Thanks

Chen

Why We Need Another Mapping Framework — vis4.net (Jun 03, 2012)

[…] attention from time to time. In 2009 I started my work in the field by porting the PROJ.4 library to ActionScript. My first notable interactive map application was a world map widget for the Piwik Analytics […]

Embed .shp Datei - Flashforum (Aug 13, 2012)

[…][...]